4339: 驾车旅行
时间限制: 1 Sec 内存限制: 128 MB提交: 1 解决: 1
[提交][状态][讨论版][命题人:]
题目描述
Freda和Rainbow一起驾车出游,这天,他们来到了Poetic Island市。
Poetic Island的街道纵横交错,南北方向和东西方向的双向街道各有n条,相邻街道的
距离均为L英里。同时,每条街道有它自己的最高速度限制。
当然,这2*n条街道构成了n*n个十字路口,其中西南角交叉口的坐标为(1,1),东北角
交叉口的坐标为(n,n)。在所有交叉口均可任意改变行驶方向,但是只能在交叉口处改变速度。
现在,Rainbow和Freda要从交叉口(sx,sy)开车行驶到(tx,ty)。他们只想沿着路程最短的
线路行驶,并且行驶时间必须在给定的闭区间[t1,t2]分钟内,车速必须是5的正整数倍。若
车速为v千米/小时,则每升汽油能行驶的路程为80-0.03v2千米。
Rainbow想知道最早到达终点的方案是什么,Freda想知道最省油的方案是什么。但是
Rainbow和Freda简直弱爆了有木有,请你帮他们计算一下吧……
输入
输入共四行
第一行为两个整数n, L。
第二行包含n个正整数,从南到北描述n条东西走向的街道的速度限制。
第三行包含n个正整数,从西到东描述n条南北走向的街道的速度限制。
第四行包含六个正整数sx, sy, tx, ty, t1, t2。
输出
若有解,输出两行,分别描述最早到达的方案(若有多种方案,选择其中最省油的)和 最省油的方案(如果有多种方案,选择其中最早到达的)。每种方案用两个数表示,第一个 数表示用时多少分钟(向上取整);第二个数表示耗油量多少升(四舍五入保留两位小数)。
若无解,仅输出一行:No。
样例输入
6 20
30 40 50 50 50 50
50 50 50 50 50 40
1 1 6 6 300 320样例输出
300 6.25
318 5.60提示
对于20%的数据,n<=4;
对于50%的数据,n<=8;
对于100%的数据,1<=n<=10, 1<=L<=20, 0<=t1<=t2<=1000,各条路速度限制不超过50;
样例说明:
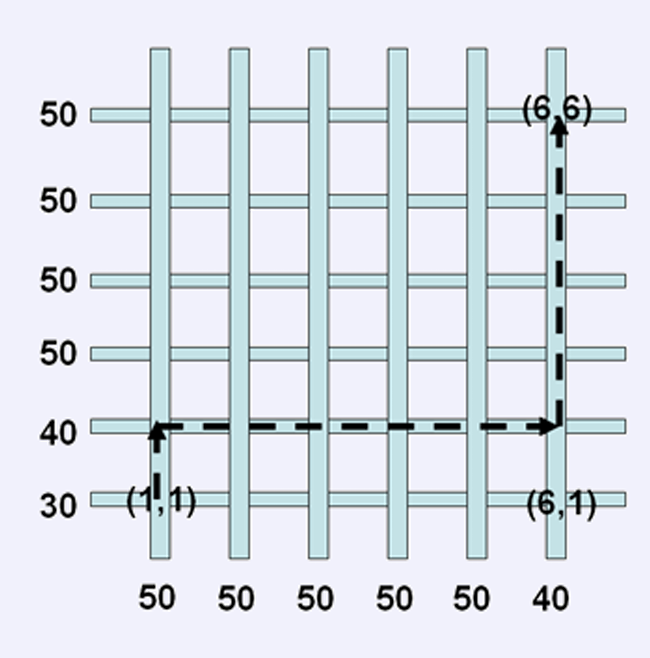
在满足题目限制条件的前提下,样例的最快路线为以40千米/小时为速度匀速前进,路
程为200 千米,因此时间为5小时,每升汽油可以行驶80-0.03*40*40=32 千米,因此耗油
量为200/32=6.25 升。最省油路线是先以40千米/小时行驶120千米,然后以35千米/小时
行驶80千米,耗油量为120/32+80/(80-0.03*35*35)=5.60 升。下图的路线可以同时满足两种
方案(其中第二种方案需要在(6,2)处改变速度)。