有 N座山排成一排,从左到右依次编号为 1∼N。
其中,第 i 座山的高度为 hi。
对于一段连续的山脉,我们使用如下方法定义该段山脉的不对称值。
如果一段连续的山脉由第 l∼r(1≤l≤r≤N)座山组成,那么该段山脉的不对称值为 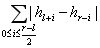
现在,你需要回答 N个问题,问题编号 1∼N。
其中,第 i个问题的内容是:请计算,一段恰好包含 i 座山的连续山脉(即长度为 i 的连续区间)的不对称值的最小可能值。
有 N座山排成一排,从左到右依次编号为 1∼N。
其中,第 i 座山的高度为 hi。
对于一段连续的山脉,我们使用如下方法定义该段山脉的不对称值。
如果一段连续的山脉由第 l∼r(1≤l≤r≤N)座山组成,那么该段山脉的不对称值为 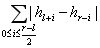
现在,你需要回答 N个问题,问题编号 1∼N。
其中,第 i个问题的内容是:请计算,一段恰好包含 i 座山的连续山脉(即长度为 i 的连续区间)的不对称值的最小可能值。
第一行包含一个整数 N。
第二行包含 N 个整数 h1,h2,…,hN。
7
3 1 4 1 5 9 20 2 0 5 2 10 10
样例1解释
关于第 5个问题的答案为什么是 2,见如下解析。
让我们依次列举所有长度为 55 的连续区间并计算区间不对称值:
由上可知,不对称值的最小可能值为 2。
数据范围
1≤N≤5000,