设有 n×m 的方格图，每个方格中都有一个整数。
现有一只小熊，想从图的左上角走到右下角，每一步只能向上、向下或向右走一格，并且不能重复经过已经走过的方格，也不能走出边界。
小熊会取走所有经过的方格中的整数，求它能取到的整数之和的最大值。
现有一只小熊，想从图的左上角走到右下角，每一步只能向上、向下或向右走一格，并且不能重复经过已经走过的方格，也不能走出边界。
小熊会取走所有经过的方格中的整数，求它能取到的整数之和的最大值。
问题 E: 方格取数
时间限制: 1 Sec 内存限制: 256 MB提交: 88 解决: 16
[提交][状态][讨论版][命题人:]
题目描述
输入
第 1 行两个正整数 n,m。
接下来 n 行每行 m 个整数，依次代表每个方格中的整数。
接下来 n 行每行 m 个整数，依次代表每个方格中的整数。
输出
一个整数，表示小熊能取到的整数之和的最大值。
样例输入
样例1
3 4
1 -1 3 2
2 -1 4 -1
-2 2 -3 -1
样例2
2 5
-1 -1 -3 -2 -7
-2 -1 -4 -1 -2样例输出
样例1
9
样例2
-10提示
数据范围
对于 20% 的数据，n,m≤5。
对于 40% 的数据，n,m≤50。
对于 70% 的数据，n,m≤300。
对于 100% 的数据，1≤n,m≤1000。方格中整数的绝对值不超过 10^4。
样例1解释
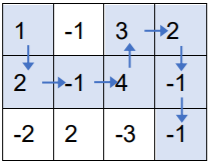
按上述走法，取到的数之和为 1+2+(−1)+4+3+2+(−1)+(−1)=91+2+(−1)+4+3+2+(−1)+(−1)=9，可以证明为最大值。
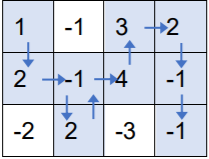
注意，上述走法是错误的，因为第 2行第 2 列的方格走过了两次，而根据题意，不能重复经过已经走过的方格。
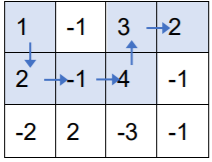
另外，上述走法也是错误的，因为没有走到右下角的终点。
样例2解释
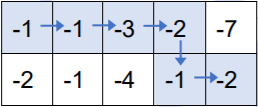
按上述走法，取到的数之和为 (−1)+(−1)+(−3)+(−2)+(−1)+(−2)=−10(−1)+(−1)+(−3)+(−2)+(−1)+(−2)=−10，可以证明为最大值。
因此，请注意，取到的数之和的最大值也可能是负数。